2269. Компоненты связности
Задан неориентированный невзвешенный граф. Найдите количество
его компонент связности.
Вход. В первой строке задано число вершин n (n ≤ 100). Далее следуют n строк по n чисел – матрица
смежности графа. В i-й строке на j-й позиции
стоит 1, если вершины i и j соединены ребром, и 0 в противном случае. На главной диагонали матрицы стоят нули. Матрица симметрична
относительно главной диагонали.
Выход. Выведите одно число – количество компонент связности
данного графа.
|
Пример
входа |
Пример
выхода |
60 1 1 0 0 01 0 1 0 0 01 1 0 0 0 00 0 0 0 1 00 0 0 1 0 0
0 0 0 0 0 0 |
3 |
РЕШЕНИЕ
графы –
компоненты связности
Анализ алгоритма
Для нахождения
количества компонент связности в графе можно использовать систему
непересекающихся множеств (Union-Find).
Сначала каждая
вершина помещается в собственное множество, и каждая из них является его
представителем. Затем для каждого ребра (u, v) объединяются
множества, содержащие вершины u и v. После обработки всех рёбер
число компонент связности равно количеству множеств в системе.
Эту задачу можно
решить и другим способом – с помощью поиска в глубину. В этом случае количество
запусков процедуры dfs будет совпадать с числом компонент связности графа.
Пример
Приведенный в примере граф имеет следующий вид:
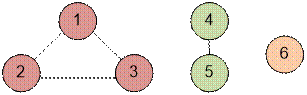
Изначально каждую вершину помещаем в отдельное
множество, где она выступает представителем.
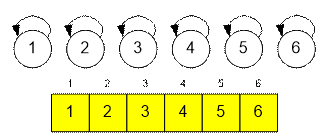
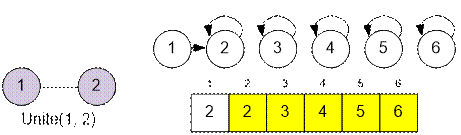
Затем
для каждого ребра (u, v) объединяем множества, содержащие
вершины u и v. После обработки всех рёбер две вершины будут
принадлежать одной компоненте связности, если у них совпадает представитель.
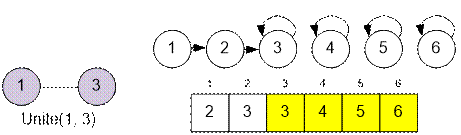
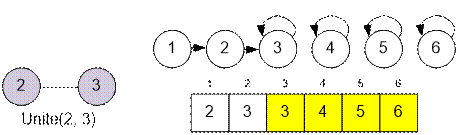
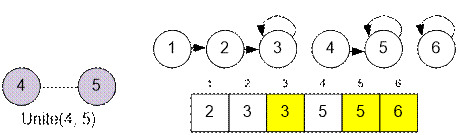
Количество
компонент связности совпадает с числом множеств в системе непересекающихся
множеств. Это число определяется количеством представителей – тех
вершин v, для которых выполняется условие parent[v]
= v.
В
приведённом примере представителями являются вершины 3, 5 и 6. Следовательно,
граф содержит три компоненты связности.
Реализация алгоритма
MAX хранит максимальное
количество вершин в графе. В массиве mas[i] записан номер вершины, на
которую указывает вершина i.
#define MAX 102
int mas[MAX];
Функция Repr возвращает
вершину-представителя множества, к которому принадлежит вершина n. Для
этого по указателям последовательно переходим к следующему элементу, пока не
дойдём до представителя множества (его указатель указывает на него самого).
int Repr(int
n)
{
while (n !=
mas[n]) n = mas[n];
return
n;
}
Функция Union объединяет два множества,
содержащие вершины x и y. Сначала находятся их представители – пусть
это будут x1 и y1. Если x1 = y1, то вершины уже принадлежат одному
множеству, и дополнительных действий не требуется. В противном случае указатель
представителя x1 перенаправляется на y1.
void Union(int
x,int y)
{
int x1 =
Repr(x),y1 = Repr(y);
if (x1 == y1)
return;
mas[x1] = y1;
}
Основная часть программы. Изначально каждая вершина
указывает сама на себя (mas[i] = i).
scanf("%d",&n);
for (i = 1; i <=
n; i++) mas[i] = i;
Читаем матрицу смежности. Для каждого ребра (i, j),
где i < j, выполняем объединение множеств, содержащих вершины i и j.
for (i = 1; i <=
n; i++)
for (j = 1; j <=
n; j++)
{
scanf("%d",&value);
if (i > j)
continue;
if (value)
Union(i,j);
}
В переменной count
подсчитываем количество
компонент связности. Это число совпадает с количеством вершин-представителей
множеств, то есть тех, которые указывают сами на себя.
count = 0;
for (i = 1; i <=
n; i++)
if (mas[i] ==
i) count++;
Выводим ответ.
printf("%d\n",count);
Реализация
алгоритма – поиск
в глубину
Объявим рабочие массивы.
#define MAX 102
int g[MAX][MAX], used[MAX];
Функция dfs выполняет
обход графа в глубину, начиная с вершины v.
void dfs(int v)
{
used[v] = 1;
for (int i = 0; i < n; i++)
if (g[v][i]
&& !used[i]) dfs(i);
}
Основная часть программы. Читаем
входные данные.
scanf("%d",&n);
for(i = 0; i < n; i++)
for(j = 0; j < n; j++)
scanf("%d",&g[i][j]);
В переменной res подсчитываем количество компонент связности.
res = 0;
Запускаем поиск в глубину на
несвязном графе. Каждый запуск функции dfs начинается с ещё
не посещённой вершины, поэтому количество вызовов dfs совпадает с
числом компонент связности графа.
memset(used,0,sizeof(used));
for (i = 0; i < n; i++)
if (!used[i])
{
dfs(i);
res++;
}
Выводим ответ.
printf("%d\n",res);
Java реализация – dfs
import java.util.*;
public class Main
{
static int g[][], used[];
static int n;
static void dfs(int v)
{
used[v] = 1;
for(int i = 1; i <= n; i++)
if (g[v][i] == 1 && used[i] == 0) dfs(i);
}
public static void main(String[] args)
{
Scanner con = new Scanner(System.in);
n = con.nextInt();
g = new int[n+1][n+1];
used = new int[n+1];
for(int i = 1; i <= n; i++)
for(int j = 1; j <= n; j++)
g[i][j] = con.nextInt();;
int res = 0;
for(int i = 1; i <= n; i++)
if (used[i] == 0)
{
dfs(i);
res++;
}
System.out.println(res);
con.close();
}
}
Java реализация – dsu
import java.util.*;
public class Main
{
static int mas[];
static int n;
static int Repr(int n)
{
while (n != mas[n]) n = mas[n];
return n;
}
static void Union(int x,int y)
{
int x1 = Repr(x);
int y1 = Repr(y);
if (x1 == y1) return;
mas[x1] = y1;
}
public static void main(String[] args)
{
Scanner con = new Scanner(System.in);
n = con.nextInt();
mas = new int[n+1];
for(int i = 1; i <= n; i++) mas[i] = i;
for(int i = 1; i <= n; i++)
for(int j = 1; j <= n; j++)
{
int val = con.nextInt();
if (i > j) continue;
if (val == 1) Union(i,j);
}
int count = 0;
for(int i = 1; i <= n; i++)
if (mas[i] == i) count++;
System.out.println(count);
con.close();
}
}
Python реализация – dsu
Функция Repr возвращает
вершину-представителя множества, к которому принадлежит вершина n. Для
этого по указателям последовательно переходим к следующему элементу, пока не
дойдём до представителя множества (его указатель указывает на него самого).
def Repr(n):
while (n !=
mas[n]): n = mas[n]
return n
Функция Union объединяет два множества,
содержащие вершины x и y. Сначала находятся их представители – пусть
это будут x1 и y1. Если x1 = y1, то вершины уже принадлежат одному
множеству, и дополнительных действий не требуется. В противном случае указатель
представителя x1 перенаправляется на y1.
def Union(x, y):
x1
= Repr(x)
y1
= Repr(y)
if (x1 == y1): return
mas[x1] = y1
Основная часть программы. Изначально каждая вершина
указывает сама на себя (mas[i] = i).
n = int(input())
mas = [int(i) for i in range (n + 1)]
Читаем матрицу смежности. Для каждого ребра (i, j),
где i < j, выполняем объединение множеств, содержащих вершины i и j.
for i in range(1,n + 1):
lst = [0] + [int(j) for j in input().split()]
for j in range(1, n + 1):
if (i < j and lst[j] == 1): Union(i, j)
В переменной res
подсчитываем количество
компонент связности. Это число совпадает с количеством вершин-представителей
множеств, то есть тех, которые указывают сами на себя.
res = 0
for i in range(1, n + 1):
if (mas[i] == i):
res += 1
Выводим ответ.
print(res)
Python реализация – dfs
Функция dfs выполняет обход графа в глубину,
начиная с вершины v.
def dfs(v):
used[v] = 1
for
i in range(n):
if
g[v][i] and not used[i]:
dfs(i)
Основная часть программы. Читаем входные данные.
n = int(input())
g = [[0] * n for _ in range(n)]
used = [0] * n
for i in
range(n):
row = list(map(int, input().split()))
for
j in range(n):
g[i][j] = row[j]
В переменной res подсчитываем количество компонент
связности.
res = 0
Запускаем поиск в глубину на несвязном графе. Каждый запуск функции dfs
начинается с ещё не посещённой вершины, поэтому количество вызовов dfs
совпадает с числом компонент связности графа.
for i in
range(n):
if
not used[i]:
dfs(i)
res += 1
Выводим ответ.
print(res)